Introduction

Game theory is the formal study of decision being made by multiple players must make choices that potentially affect the interests of the other players. Now, game theory can be used to describe how football player’s agents and football clubs should maximise their payoff, which can be defined as the profit or utility (points in the league table), while cooperating with each other. So, as you may have guessed by now, I will be focusing on cooperative game theory in this essay, but we will dip in and out of non-cooperative game theory too as agents are not paid to be nice. But let us first get a feel for the market of players to do proper economic analysis.

Market for players

Agents, who represent both the players and the club’s interest, are the sellers in this market. Their incentive is to maximise the transfer fee and the agreed salary of the player as the agent gets a cut from the year’s wages and a slice of the transfer fee paid for the player’s services. They also have to think about sponsors. The agent needs to negotiate the split between the club and the player on the fees earned by sponsors, and this is especially important for star players. Football agents have a key role to play in increasing the financial power currently experienced by footballers. For example, due to a good season for his club, a player’s market value goes up so his agents will often use this as a bargaining tool to engineer a new contract for that player despite not being anywhere near the end of his previous contract. Football player’s contracts can last for a total of five years but are often renewed after only two years in order to increase the wages paid to that player – this is a key example of player power.

The Price Elasticity of Demand is low for football players, especially in the premier league, although the elasticity varies depending on the club. The richest clubs usually have higher reservation price for the player they target, and their PED is usually inelastic as they are keen to improve their team. For example, in 2015, Manchester City paid £49 million for Raheem Sterling in 2015, while Leicester City paid £375,000 for Mahrez in 2014. Mahrez was one the top goal scorer for Leicester with 19 goals and 11 assists, while Sterling exhibited a relatively meagre performance of 11 goals and 4 assists (and then helped England exit Europe). So obviously, the utility derived by Leicester (which went on to win the latest premier league, partly due to the magic of Mahrez) was much higher than that of Manchester City, though his initial prize was much lower.

[i]Transfer fees serve to prevent a total barrier for players’ mobility. Free movement of players is restricted under transfer rules so that there is a fair and balanced competition. This is so that clubs experiencing a string of success are not able to attract the suddenly best players in the league and drain their competitors.

Game theory in negotiation of transfer fee

When we use game theory in economic analysis, we assume these things:

· Players or parties rational beings.

· Players have the intention to maximize their utility/outcome.

· Players will accept the highest payoffs (profit or utility).

· Players know the "rules of the game.", which means that they have full knowledge on how the game is operating

· Players assume other parties to be fully rational.

· The number of players is fixed and known to all parties.

· Each party recognizes a set of available options and develops tangible preferences among those options. Preferences remain constant throughout the conflict/negotiation interaction.

· Each party knows or can estimate well the options and preferences of the other parties.

· Communication is limited, highly controlled, or not relevant to the conflict/negotiation interaction.

· A decision must be possible that is maximally efficient, i.e., intersects with the solution set at a point that maximizes each party's own interests (so too create a pareto optimal, which is the allocation of resources in a way so that it is impossible for one individual to be better off without making at least one individual worse off).

Now, let us imagine a black box. Imagining this black box is important as it represents the apparatus of the legal system (set by completely reliable and controversial-free regulatory bodies like FIFA), and we have to assume that there is cooperation as the both sides of the table could get sued if they don’t live up to their side of their bargain. So from the the following discussion, we are going to imagine the existence of this black box so that we can simplify the problem at hand.

The simplest two-person game

Usually when we think of negotiations, we imagine two people facing off against each other. Whatever one wins, the other loses the same amount. So, in regards to the question, in the negotiations the player’s agent wants to maximise his/her compensation and the buying club wants to minimise the fee it offers for the player.

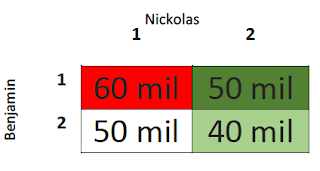
In the following example, let’s say Nickolas is the manager of Jamie’s Angels F.C., and is negotiating the transfer Dmitri Lafayette from City Hawks and they have to agree on how much JAFC will pay for Lafayette with his agent, Benjamin. They each have two strategies available to them, but the outcome is not just dependent on the strategy chosen, but also on what their opponent does. So while Nickolas would obviously choose to pay the minimum (£40,000,000) and Benjamin would like to have the maximum (£60,000,000), the opposing move needs to be taken into account before an optimal strategy can be selected.

As the title of this section might suggest, this game might be the simplest negotiation scenario we could think of. The minimax theorem would tell us that these rational agents of economic force should pick the strategy where the maximum advantage of their opponent is minimized. So, in the above example, Nickolas should pick strategy #2 to pay 10 less unit (a unit being 10 million) while Benjamin should pick strategy #1 to avoid only getting paid 40 million.

The Minimax theorem is a simple but useful as it can be can be applied to everyday situations. However, it’s problematic partly because it assumes the parties have access to perfect information. Obviously, real life is much more complicated, not least because our negotiating opponent is rarely limited to two strategies.

Let’s see what happens if we add additional strategic possibilities.

Although much more complicated, this game is still solvable. It is generally an advantage to have less options for yourself and more options for your opponent (although a bit counter-intuitive).

Game theorists achieve this mathematically by determining which strategies are numerically dominant and using randomly mixed strategies. During negotiation, the agent or the buying club would calculate h have a clear idea of what you want and eliminate inferior options. Your advantage can sometimes be increased if you don’t announce your preferences to your opponent so that he still has to consider variables which you don’t.

Nash bargaining solution

So Lafayette is worth £60,000,000 (this would be its reservation price, which the highest price a consumer is willing to offer for a good or service) to the JAFC while the Hawks would be willing to sell Lafayette for at least £40,000,000. So, how can the cooperatively share the surplus of £20,000,000 amongst themselves. Now, the common approach to this problem would be to say that the player would be sold at £50,000,000, so the surplus is shared equally. However, each side could take advantage of their positions for a non-equilibrium (or zero sum) outcome to be produced. It could be that the Lafayette is very eager to move to Jamie’s Angels so the agent might be under pressure to let a deal go through as quickly as possible to avoid the risk of losing the transfer. However, if the agent knows JAFC is desperate for Lafayette and that Lafayette is in high demand, then he would be willingly to take more risk and demand a higher surplus.

Nash figured out the the set of agreement would be shaped like curved rectangle as Nickolas lie a curved square or a circle as Benjamin and Nickolas would be willingly to take different levels of risk differently, as we can see for figure 3. Another way to look at this would be say that Benjamin and Nickolas have different The Pareto frontier (the line of efficient outcomes) would be across the edge of the possible agreements. We would draw a tangent to the point which is the midpoint of the frontier, and set the slope’s angle to 45°. So the picture is looking quite pretty at the moment.

Let’s play with some numbers (aha pun, get it?). Let’s get back to how the two parties value the transfer of Lafayette. JAFC believes that Lafayette can get them points in the next season if they bring him in, as he is a top notch goal scorer. This also means that the demand for Lafayette is very high as he is a very well known player. Due to his ability to bring points to his team (the extra nine points would most likely that they would finish second in the league next season) they would get 15 million more from the Premier League, and the revenue from shirts, sponsorship and increased tickets is estimated to be around 15 million. So, the utility for buying Lafayette for JAFC would be 30 utils (this an arbitrary unit of utility defined as £1 million for 1 util). But for every 10 million more they invest into Lafayette’s transfer from City Hawks asking price, they lose 3 utils. Now, City Hawks, would be able to afford one extra defender who will give them 2 points each for every 20 million they would earn from the deal. 5 points would move them one place up in the table from the third place, and they would earn £6 million from every place they move up, which is 6 utils. Now, the two extremes are that JAFC pays the Hawks £40 million, or that it pays the Hawks £60 million.

· In the first extreme, the JAFC gain 30 – 4*3 = 18 utils. Hawks would be able to buy two defenders, and so it will gain 12 utils.

· In the second extreme, the JAFC will gain 30 - 6*3 = 12 utils. Hawks will be able to buy three defenders, so it would gain 18 utils.

Nash’s bargaining solution is found by averaging the two extremes. The average gives 15 utils for City Hawks and also 16 utils for Jamie’s Angels. This means the price should be at £50 million. Conveniently, the artificial numbers in this hypothetical scenario turned out to work so that the answer came out to be the nice average £50 million, but under different conditions, the Nash’s bargaining solution would have been the most realistic way to compute the ultimate transfer fee than finding the average of the maximum and minimum prices being offered by the negotiators.

Rubenstein’s bargaining method

We have not considered commitment issues. If, let’s say, Benjamin is intent that he will only accept at least a bid of £55 million for Lafayette’s, what guarantee would Nickolas have that this is Benjamin’s lowest asking price. This is a negotiation after all. Ben and Nick can alternate offers until they reach an agreement. Assuming that the prefer to make a particular deal now then later, then Rubenstein showed that there is a sub-game perfect equilibrium. If Nick is more patient then Ben, his discount rate (the rate at which he decreases his price to sell Lafayette) would be lower, so he will get a higher portion of the 20-million-pound surplus. Rubenstein’s model assumes there is perfect information, so both sides now for sure what each other minimum/maximum offers are. Neither Ben nor Nick know the most the first is willing to offer and the least the latter is willing to accept for Lafayette. The issue of commitment means that both parties stand to benefit from being patient, but due to the nature of the transfer market of the premier leagues (Lafayette has to be sold during the transfer window), time is a limited resources and demand for Lafayette is high, so JAFC’s Nickolas would cannot afford the same patience as Benjamin because delays are costly.

Let’s answer one final question with game theory about the transfer of players.

Should a football team sell a player?

The club has to calculate the expected value of selling a player or not to look at this question.

EV(Not sell) = P(Club staying in EPL) x (Total Revenue from EPL) + P(Relegated) x (Total Revenue from the Championship) – (Money spent improving the squad)

EV(Sell) = P(Staying in the EPL) * (Total Revenue from being in the EPL) + P(Relegated) x (Total Revenue from the Championship) + (Money gained from selling) – (Money spent replacing him)

Note: EV stands for Expected Value

But, the intangible value that a player can bring to the club should be considered too. For example, Lafayette brings the City Hawks a loyal fan base who are excited to see their star player and so are more likely to come frequently to matches. Then, there is also the morale that the star player Lafayette brings to the changing room and chemistry on to the field, so that the team is motivated and able to win matches. Considering these, it might not be such a good idea for a Nickolas to sell Lafayette. If we quantify these costs as revenue in form of ticket, merchandise and earnings from winning games, these costs would be the opportunity cost of selling Lafayette.